554. Inscribed circle
The circle is inscribed in
a polygon, if it has a point of contact with each side of the polygon.
Determine is it possible to
inscribe a circle into a given convex polygon, and if the answer is positive,
find the coordinates of its center and radius.
Input. The first line contains the
number of vertices of the polygon n (3 ≤
n ≤ 8). The following n lines contain the coordinates of the
vertices of the polygon in order circumvent anti-clockwise, each line contains
two integers: xi and yi that do not exceed 1000 by
absolute value.
Output. If an inscribed circle in
polygon exist, print in the first line the word YES, otherwise print the
word NO. If answer is yes, print in the second row the coordinates of the
circle center and its radius. Print the answer with accuracy 10-6.
|
Sample input |
Sample output |
|
4 0 0 1 0 1 1 0 1 |
YES 0.500000
0.500000 0.500000 |
SOLUTION
geometry
Algorithm analysis
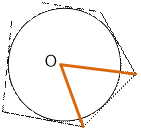
Construct the
bisectors of two adjacent corners of the polygon and find the point (xc, yc) of their intersection. If a circle can be inscribed
into the
polygon, then this point will be its center. Compute the radius of the circle r. Find the distances from (xc, yc) to all sides of the polygon. If they all equal to r, then a circle can be inscribed in the polygon. Otherwise no.
Let a1 x + b1 y + c1 = 0 and a2 x
+ b2 y + c2 = 0 be the equations of the sides of an angle. Then the
equation of the angle bisector (as a geometric set of points equidistant from
the sides of the angle) has the form:
 =
= 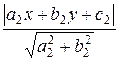
Algorithm realization
The coordinates (xi, yi) of a polygon store in (x[i],
y[i]).
#define MAX 10
#define EPS 1e-7
int
x[MAX], y[MAX];
Function Bisect finds the equation of the bisector ax + by
+ c = 0 of the angle of the
polygon at the vertex (xn,
yn) (that is, the angle
between the sides (xn-1,
yn-1) – (xn, yn) and (xn, yn) – (xn+1,
yn+1) ).
void
Bisect(int n, double
&a, double &b, double
&c)
{
Rename the points.
double x0 =
x[n-1], y0 = y[n-1];
double x1 =
x[n], y1 = y[n];
double x2 =
x[n+1], y2 = y[n+1];

The equation of the line AB is  =
=  or
or
(y1 – y0)x + (x0
– x1)y + x1 y0 – x0 y1
= a1 x + b1 y + c1
= 0
The equation of the line BC:  =
=  or
or
(y2 – y1)x + (x1
– x2)y + x2 y1 – x1 y2
= a2 x + b2 y + c2
= 0
double a1 =
y1 - y0, a2 = y2 - y1;
double b1 =
x0 - x1, b2 = x1 - x2;
double c1 =
x1*y0 - x0*y1;
double c2 =
x2*y1 - x1*y2;
If a1 x + b1 y + c1 = 0 and a2 x
+ b2 y + c2 = 0 are the equations of the sides of an angle, then the equation of the angle
bisector (as a geometric set of points equidistant from the sides of the angle)
has the form:
 =
= 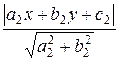
Omit the modulus, denote d1 = ![]() , d2 =
, d2 = ![]() and rewrite
the equation in the form:
and rewrite
the equation in the form:
![]() =
= ![]() ,
,
![]() =
= ![]() = 0
= 0
double d1 =
sqrt(a1*a1 + b1*b1);
double d2 =
sqrt(a2*a2 + b2*b2);
a = a1 * d2 - a2 * d1;
b = b1 * d2 - b2 * d1;
c = c1 * d2 - c2 * d1;
}
Solve a system of
linear equations by Cramer’s rule. Since
two adjacent bisectors always intersect, we will not track the case when the
system of equations has no (infinitely many) solutions.
void
kramer(double a1,double
b1, double c1,
double a2, double
b2, double c2, double
&x, double &y)
{
double d = a1
* b2 - a2 * b1;
double dx =
c1 * b2 - c2 * b1;
double dy =
a1 * c2 - a2 * c1;
x = dx/d; y = dy/d;
}
The distance from the point (x, y)
to the line ax + by + c
= 0 equals to
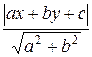
double dist(double a, double b, double c, double x, double y)
{
return
fabs(a*x+b*y+c) / sqrt(a*a + b*b);
}
The main part of the program. Read
the input data.
scanf("%d",&n);
for(i
= 0; i < n; i++)
scanf("%d
%d",&x[i],&y[i]);
x[n]
= x[0]; y[n] = y[0];
Find the equations of the
bisectors of the first and second angles.
Bisect(1,a1,b1,c1);
Bisect(2,a2,b2,c2);
Using Cramer’s method, find the intersection point of the bisectors (xc, yc). Compute the radius r of the required
circle as the distance from the center (xc, yc) to the line (x0, y0) – (x1,
y1) (the existence of the circle itself will be
checked later).
kramer(a1,b1,-c1,a2,b2,-c2,xc,yc);
r
= dist(y[1] - y[0],x[0] - x[1],x[1]*y[0] - x[0]*y[1],xc,yc);
Compute the distances from the point (xc, yc) to all sides of the polygon. If they all equal to r, then a circle inscribed in the polygon exists.
for(i
= 1; i < n; i++)
{
d = dist(y[i+1] - y[i], x[i] -
x[i+1],x[i+1]*y[i] - x[i]*y[i+1],xc,yc);
if (fabs(d -
r) > EPS)
{
printf("NO\n");
return 0;
}
}
Print the center and the radius of the
desired inscribed circle.
printf("YES\n");
printf("%.6lf %.6lf %.6lf\n",xc,yc,r);